Risk Averse Blackjack Indexes

Deviations from basic strategy based on the true count (actually there are three that use the running count, namely 16 v T, ES 14 v T, and 12 v 4) are known as index plays. Traditionally, index plays are EV maximizing, and that is certainly the right approach. Most of the time. But what if other metrics were also important?

The theory behind risk-averse indexes is that by reducing a bit of the variance in blackjack, you can actually bet more aggressively before the hand is dealt and end up with a higher hourly. This is especially important for full Kelly bettors, who are exposing themselves to a lot of variance.

Some Risk-Averse Index Plays

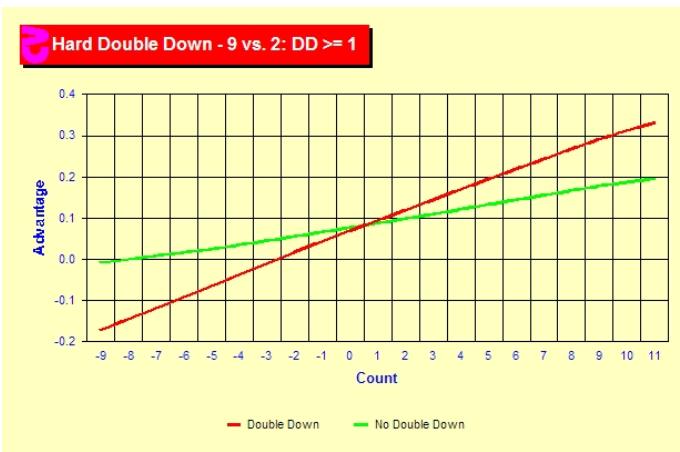
9 v 2, 7

Note on the above image, at TC+1 the lines intersect. However, the gap widens quickly, and by TC+2 there is already a +3% difference. Note, however, that this is easily a play where you could be betting at TC+2 or TC+3 and have the index drop by the time it is your turn to make your play. In this situation, when you are at TC+1 but with a TC +3 bet on the table, it becomes imperative to hit instead of doubling, because the variance cost is so much higher for no gain in expectation.

Normally you double 9 v 2 at +1 and 9 v 7 at +3. However, these are plays with a lot of variance, especially 9 v 7, because often you are going to wish that you could have taken a second card (if you catch a 2-7). Instead, the risk-averse indexes is to double at +2 and +5 respectively.

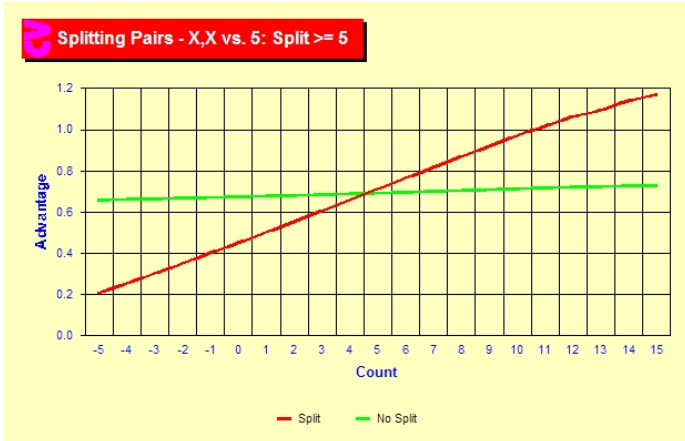
Splitting tens

Splitting tens is another risk-averse index play. I wait until +7 and then split both TT v 5 and 6. I do not split TT against 4 or below. I also won't resplit unless the true count is +8 or above. Note that by TC +7 there is a 10% difference in EV between staying and splitting, and that difference escalates rapidly at higher counts. By TC+10 there is a 35% difference.

A6 v 2.

The EV maximizing index with A6 v 2 is +1. However, the problem here is that the gain in expectation is negligible. Furthermore, Hilo is not very well correlated to this decision. We actually want to see more 2s, 3s, and 4s available to us - which is something that would happen in a low count, not a high count. Furthermore, the density of 7s, 8s, and 9s is also very important since those are the cards that the dealer wants. All of this means that unlike 10 v 5, a decision that is highly correlated to the true count, A6 v 2 is not correlated to the true count. So even at high counts, doubling means a lot more  variance, for not much gain in advantage. 

Therefore, the risk averse index for A6 v 2 is to simply not double!

10 v T

The Hilo ev maximizing index for this play is +4. However, this is a play with a lot of variance. We do have one advantage here, which is we know the dealer does not have blackjack. Still, in a high count, the dealer is going to end up with 20 just as often as we are. This is a play with a lot of risk but not a lot of reward. However, it is a play that is correlated to the count, because we can hit either an ace or a ten and the dealer has already shown they do not have an ace in the hole. 

If you look at the graphic above, we see only the slightest space between the red line and the green line at TC+4. The gain is minuscule, maybe 1%. By TC+7 you are looking at a 3% or 4% difference in advantage.

Therefore, the risk-averse index for 10 v T is to double at +7. 

This is especially valid if you do as most counters do and cap out your max bet at TC + 4 or TC +5. That means at TC + 7 you are incurring exactly as much risk as you would at TC + 4, but for substantially more reward. As opposed to someone who continued to increase their wagers at higher true count, who would be taking on more risk for more reward.

Risk Averse Insurance

Conventional card counter wisdom says that insurance is just an irrelevant side bet. Take it at the insurance index, don't before. However, there is some ploppy wisdom to insuring hands like 20. Taking insurance with a count of 20 substantially reduces our variance. The only way we lose is if the dealer hits to 20, in which case we tie, or 21. That's pretty unlikely with an ace up. So insuring a hand like 20 does decrease our variance. Conversely, insuring a total of 16 increases our variance, since we can easily lose the insurance bet and then lose our hand.

Now, how can we implement this in an intelligent manner?

One approach is to insure a total of 20 slightly before the index. For example, if the true count is +2 or higher, we insure TT or A9. The cost to insure is minimal since we are near the index already, and it should reduce our variance. Taking even money at TC + 2 or higher would also reduce our variance somewhat. Further, we refuse to insure a total of hard 16 or hard 15 until slightly after the index, like TC 3.5.